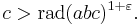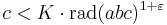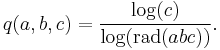abc conjecture

The abc conjecture (also known as Oesterlé–Masser conjecture) is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser in 1985. The conjecture is stated in terms of three positive integers, a, b and c (whence comes the name), which have no common factor and satisfy a + b = c. If d denotes the product of the distinct prime factors of abc, the conjecture essentially states that d is rarely much smaller than c.

Although there is no obvious strategy for resolving the problem, it has already become well known for the number of interesting consequences it entails. Dorian M. Goldfeld described the abc conjecture as "the most important unsolved problem in Diophantine analysis".^[1]

Unsolved problems in mathematics
Are there for every ε > 0, only finitely many triples of coprime positive integers a + b = c such that c > d^(1+ε) where d denotes the product of the distinct prime factors of abc?

1 Formulations
2 Examples of triples with small radical
3 Some consequences
4 Theoretical results
5 Computational results
6 Refined forms and generalizations
7 See also
8 Notes
9 Further reading
10 External links

Formulations

For a positive integer n, the radical of n, denoted rad(n), is the product of the distinct prime factors of n. For example

rad(16) = rad(2⁴) = 2,
rad(17) = 17,
rad(18) = rad(2·3²) = 2·3 = 6.

If a, b, and c are coprime^[2] positive integers such that a + b = c, it turns out that "usually" c < rad(abc). The abc conjecture deals with the exceptions. Specifically, it states that for every ε>0 there exist only finitely many triples (a,b,c) of positive coprime integers with a + b = c such that

$c>\operatorname{rad}(abc)^{1%2B\varepsilon}.$

An equivalent formulation states that for any ε > 0, there exists a constant K such that, for all triples of coprime positive integers (a, b, c) satisfying a + b = c, the inequality

$c < K \cdot \operatorname{rad}(abc)^{1%2B\varepsilon}$

holds.

A third formulation of the conjecture involves the quality q(a, b, c) of the triple (a, b, c), defined by:

$q(a, b, c) = \frac{ \log(c) }{ \log( \operatorname{rad}( abc ) ) }.$

For example

q(4, 127, 131) = log(131) / log(rad(4·127·131)) = log(131) / log(2·127·131) = 0.46820...
q(3, 125, 128) = log(128) / log(rad(3·125·128)) = log(128) / log(30) = 1.426565...

A typical triple (a, b, c) of coprime positive integers with a + b = c will have c < rad(abc), i.e. q(a, b, c) < 1. Triples with q > 1 such as in the second example are rather special, they consist of numbers divisible by high powers of small prime numbers.

The abc conjecture states that, for any ε > 0, there exist only finitely many triples (a, b, c) of coprime positive integers with a + b = c such that q(a, b, c) > 1 + ε.

Whereas it is known that there are infinitely many triples (a, b, c) of coprime positive integers with a + b = c such that q(a, b, c) > 1, the conjecture predicts that only finitely many of those have q > 1.01 or q > 1.001 or even q > 1.0001, etc.

Examples of triples with small radical

The condition that ε > 0 is necessary for the truth of the conjecture, as there exist infinitely many triples a, b, c with rad(abc) < c. For instance, such a triple may be taken as

a = 1

b = 2⁶ⁿ − 1

c = 2⁶ⁿ.

As a and c together contribute only a factor of two to the radical, while b is divisible by 9, rad(abc) < 2c/3 for these examples. By replacing the exponent 6n by other exponents forcing b to have larger square factors, the ratio between the radical and c may be made arbitrarily large. Another triple with a particularly small radical was found by Eric Reyssat:^[3]

a = 2:

b = 3¹⁰ 109 = 6436341

c = 23⁵ = 6436343

rad(abc) = 15042.

Some consequences

The conjecture has not been proven, but it has a large number of interesting consequences. These include both known results, and conjectures for which it gives a conditional proof.

Thue–Siegel–Roth theorem on diophantine approximation of algebraic numbers
Fermat's Last Theorem for all sufficiently large exponents (proven in general by Andrew Wiles)
The Mordell conjecture (proven by Gerd Faltings)^[4]
The Erdős–Woods conjecture except for a finite number of counterexamples^[5]
The existence of infinitely many non-Wieferich primes^[6]
The weak form of Marshall Hall's conjecture on the separation between squares and cubes of integers^[7]
The Fermat–Catalan conjecture, a generalization of Fermat's last theorem concerning powers that are sums of powers^[8]
The L function L(s,(−d/.)) formed with the Legendre symbol, has no Siegel zero (this consequence actually requires a uniform version of the abc conjecture in number fields, not only the abc conjecture as formulated above for rational integers)
P(x) has only finitely many perfect powers for integral x for P a polynomial with at least three simple zeros.^[9]
A generalization of Tijdeman's theorem
It is equivalent to the Granville–Langevin conjecture
It is equivalent to the modified Szpiro conjecture.
Dąbrowski (1996) has shown that the abc conjecture implies that n! + A= k² has only finitely many solutions for any given integer A.^[10]

While the first group of these have now been proven, the abc conjecture itself remains of interest, because of its numerous links with deep questions in number theory.

Theoretical results

It remains unknown whether c can be upper bounded by a near-linear function of the radical of abc, as the abc conjecture states, or even whether it can be bounded by a polynomial of rad(abc). However, exponential bounds are known. Specifically, the following bounds have been proven:

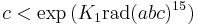$c < \exp{(K_1 \operatorname{rad}(abc)^{15}) }$ (C. L. Stewart & R. Tijdeman 1986),^[11]

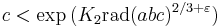$c < \exp{ (K_2 \operatorname{rad}(abc)^{2/3%2B\varepsilon}) }$ (C. L. Stewart & Kunrui Yu 1991),^[12] and

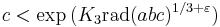$c < \exp{ (K_3 \operatorname{rad}(abc)^{1/3%2B\varepsilon}) }$ (C. L. Stewart & Kunrui Yu 2001).^[13]

In these bounds, K₁ is a constant that does not depend on a, b, or c, and K₂ and K₃ are constants that depend on ε (in an effectively computable way) but not on a, b, or c. The bounds apply to any triple for which c > 2.

Computational results

In 2006, the Mathematics Department of Leiden University in the Netherlands, together with the Dutch Kennislink science institute, launched the ABC@Home project, a grid computing system which aims to discover additional triples a, b, c with rad(abc) < c. Although no finite set of examples or counterexamples can resolve the abc conjecture, it is hoped that patterns in the triples discovered by this project will lead to insights about the conjecture and about number theory more generally.

Distribution of triples with q > 1^[14]
	q > 1	q > 1.05	q > 1.1	q > 1.2	q > 1.3	q > 1.4
c < 10²	6	4	4	2	0	0
c < 10³	31	17	14	8	3	1
c < 10⁴	120	74	50	22	8	3
c < 10⁵	418	240	152	51	13	6
c < 10⁶	1.268	667	379	102	29	11
c < 10⁷	3.499	1.669	856	210	60	17
c < 10⁸	8.987	3.869	1.801	384	98	25
c < 10⁹	22.316	8.742	3.693	706	144	34
c < 10¹⁰	51.677	18.233	7.035	1.159	218	51
c < 10¹¹	116.978	37.612	13.266	1.947	327	64
c < 10¹²	252.856	73.714	23.773	3.028	455	74
c < 10¹³	528.275	139.762	41.438	4.519	599	84
c < 10¹⁴	1.075.319	258.168	70.047	6.665	769	98
c < 10¹⁵	2.131.671	463.446	115.041	9.497	998	112
c < 10¹⁶	4.119.410	812.499	184.727	13.118	1.232	126
c < 10¹⁷	7.801.334	1.396.909	290.965	17.890	1.530	143
c < 10¹⁸	14.482.059	2.352.105	449.194	24.013	1.843	160

As of March 2011^[update], ABC@Home has found 20.9 million triples, and its present goal is to obtain a complete list of all ABC triples (a,b,c) with c no more than 10²⁰.^[15]

Highest quality triples^[16]
	q	a	b	c	Discovered by
1	1.6299	2	3¹⁰109	23⁵	Eric Reyssat
2	1.6260	11²	3²5⁶7³	2²¹23	Benne de Weger
3	1.6235	19·1307	7·29²31⁸	2⁸3²²5⁴	Jerzy Browkin, Juliusz Brzezinski
4	1.5444	7²41²311³	11¹⁶13²79	2·3³5²³953	Abderrahmane Nitaj
5	1.4805	5²²79·45949	3²13¹⁸61³	2²³17⁴251²1733³	Frank Rubin

where the quality q(a, b, c) of the triple (a, b, c), defined by:

$q(a, b, c) = \frac{ \log(c) }{ \log( \operatorname{rad}( abc ) ) }.$

Refined forms and generalizations

A stronger inequality proposed in 1996 by Alan Baker states that in the inequality, one can replace rad(abc) by

ε^−ωrad(abc),

where ω is the total number of distinct primes dividing a, b and c. A related conjecture of Andrew Granville states that on the RHS we could also put

O(rad(abc) Θ(rad(abc)))

where Θ(n) is the number of integers up to n divisible only by primes dividing n.

In 1994, Jerzy Browkin and Juliusz Brzeziński formulated the n-conjecture^[17]—a version of the abc conjecture involving $n>2$ integers.

Notes

^ Goldfeld, Dorian (1996), "Beyond the last theorem", Math Horizons (September): 26–34
^ Note that when it is given that a + b = c, coprimeness of a, b, c implies pairwise coprimeness of a, b, c. So in this case, it does not matter which concept we use.
^ Lando and Zvonkin, p.137
^ Elkies, N. D. (1991), "ABC implies Mordell", Intern. Math. Research Notices 7 (7): 99–109, doi:10.1155/S1073792891000144
^ Langevin, M. (1993), "Cas d'égalité pour le théorème de Mason et applications de la conjecture abc", Comptes rendus de l'Académie des sciences 317 (5): 441–444 (French).
^ Silverman, Joseph H. (1988), "Wieferich's criterion and the abc-conjecture", Journal of Number Theory 30 (2): 226–237, doi:10.1016/0022-314X(88)90019-4
^ Nitaj, Abderrahmane (1996), "La conjecture abc", Enseign. Math. 42 (1–2): 3–24 (French).
^ Pomerance, Carl (2008), "Computational Number Theory", The Princeton Companion to Mathematics, Princeton University Press, pp. 361–362
^ http://www.math.uu.nl/people/beukers/ABCpresentation.pdf
^ Andrzej Dąbrowski (1996), "On the diophantine equation 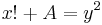$x!%2BA=y^2$ ", Nieuw Archief voor Wiskunde, IV. 14: 321–324
^ Stewart, C. L.; Tijdeman, R. (1986), "On the Oesterlé-Masser conjecture", Monatshefte für Mathematik 102 (3): 251–257, doi:10.1007/BF01294603.
^ Stewart, C. L.; Kunrui Yu (1991), "On the abc conjecture", Mathematische Annalen 291 (1): 225–230, doi:10.1007/BF01445201.
^ Stewart, C. L.; Kunrui Yu (2001), "On the abc conjecture, II", Duke Mathematical Journal 108 (1): 169–181, doi:10.1215/S0012-7094-01-10815-6.
^ "Synthese resultaten", RekenMeeMetABC.nl, http://www.rekenmeemetabc.nl/?item=h_stats, retrieved January 1, 2011 (Dutch).
^ "Data collected sofar", ABC@Home, http://abcathome.com/data/, retrieved March 20, 2011
^ "100 unbeaten triples". Reken mee met ABC. 2010-11-07. http://www.math.leidenuniv.nl/~desmit/abc/index.php?set=1.
^ J. Browkin, J. Brzeziński (1994), "Some remarks on the abc-conjecture", Math. Comp. (American Mathematical Society) 62 (206): 931–939, doi:10.2307/2153551, JSTOR 2153551

External links

ABC@home Distributed Computing project called ABC@Home.
Easy as ABC: Easy to follow, detailed explanation by Brian Hayes.
Weisstein, Eric W., "abc Conjecture" from MathWorld.
Abderrahmane Nitaj's ABC conjecture home page
Bart de Smit's ABC Triples webpage
http://www.math.columbia.edu/~goldfeld/ABC-Conjecture.pdf
The amazing ABC conjecture
The ABC's of Number Theory by Noam D. Elkies